From Math to Algorithms: Implementing Traditional Equations via Programming
TL;DR: Learn how to decode and implement mathematical equations from scientific papers using programming, unlocking the black box of computational creativity.
.png)
Background
As many of you know, Genuary 2025 has officially begun! For those unfamiliar with it, Genuary is a community-driven movement celebrating generative art. The concept is simple: each day in January comes with a unique creative prompt, inviting participants to craft algorithmic compositions inspired by the day’s theme. You can get more information about the project from the following link.
While Day 11’s prompt feels a bit daunting for me, it sparked an idea—why not write a tutorial? Specifically, I’m considering exploring how to implement scientific equations by converting polar equations into the Cartesian coordinate system. It’s a fascinating topic that blends math, coding, and art, and I’d love to share my process with the community and my students.
For this context, I chose to explore a variation of the Superformula, introduced by Johan Gielis. This mathematical equation is incredibly versatile, capable of synthesizing, modulating, and analyzing patterns such as images, sound waveforms, electromagnetic signals, and more through computational means. Acting as a linear operator, the Superformula enables the creation of diverse shapes, waveforms, and other complex representations. Its efficiency significantly enhances computational processes, offering substantial memory savings and a remarkable boost in processing power. This makes it an invaluable tool for both artistic and technical applications.
The Prompt
Day 11:Impossible day - Try to do something that feels impossible for you to do. Maybe it is impossible. Maybe it’s too ambitious. Maybe it’s something you know nothing about how to accomplish.
Step 1 - Basic Trigonometry
Before diving into the implementation of the Superformula, let’s revisit the basics of trigonometry. As a starting point, we’ll calculate the position of points on a unit circle, which is foundational for implementing more complex equations. For this tutorial, I’ll use p5.js as my creative coding tool.
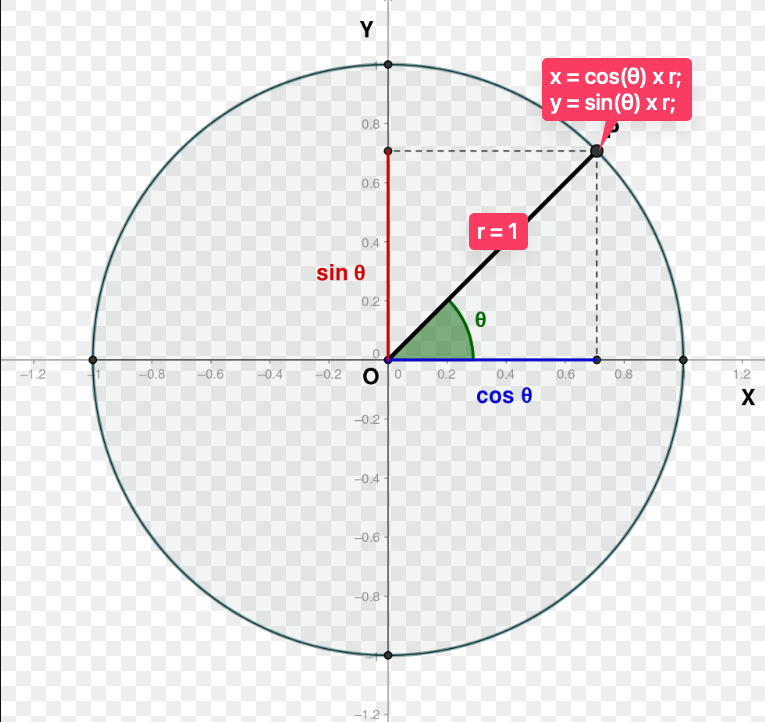
Here’s a simple example: the following code snippet draws 100 points arranged in a circular path. The radius of the circle is set to 100 pixels (r), and the total number of points is controlled by the res constant. The angle between each point, perResAngle, is calculated by dividing the full circle (2π) by the number of points (res).

const locX = width * 0.5; // x position of the circle on canvas
const locY = height * 0.5; // y position of the circle on canvas
const res = 100;
const perResAngle = TWO_PI / res;
for (let i = 0; i < res; i++) {
const r = 100; // distance of each point from the center (locX, locY)
const x = locX + cos(perResAngle * i) * r; // relative pos x of each point
const y = locX + sin(perResAngle * i) * r; // relative pos y of each point
stroke(200, 0, 0); // stroke color of each point
strokeWeight(2); // thickness of each point
point(x, y); // display each point
}This simple example prepares the foundation for more intricate patterns using mathematical formulas.
Step 2 - Implementation of The Formula
The next step involves implementing a variation of the Superformula, a concept introduced by Johan Gielis and detailed in its patent documentation. The Superformula is a powerful tool for generating complex, flower-like patterns in polar coordinates. By adjusting parameters, it allows for a wide variety of shapes.
FIGS. 11(A)-11(E) show 2-dimensional (flower-like) images, represented in polar coordinates, created by the insertion of parameters as per the respective super-formula equations shown.
Here’s the equation, where r represents the radius of the nth point on a unit circle:
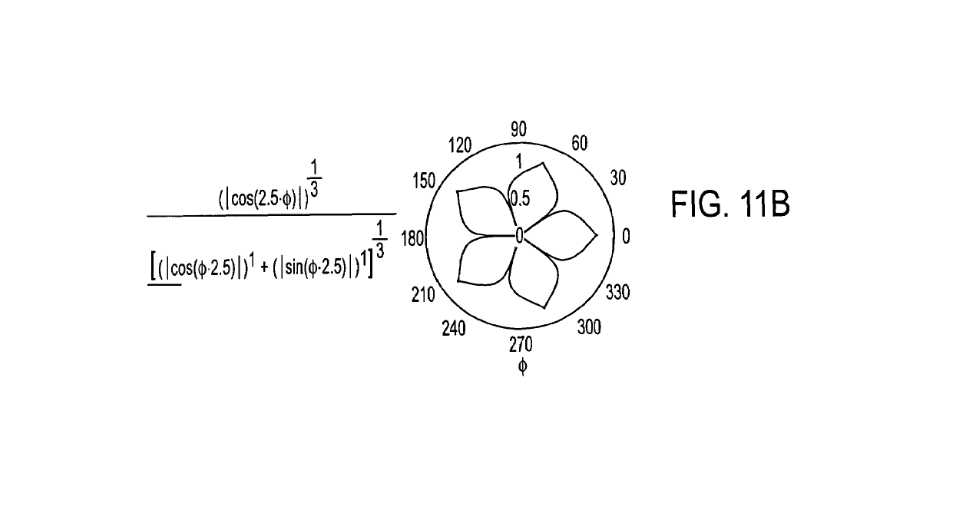
According to the following equation, it represents radius of nth point on a unit circle. So our r constant will be equal implementation of the formula. By implementing the following formula basically we adjust each point’s distance to the center location. Instead of keeping the distance of each point constant, we will adjust the position of each point according to the equation to get flower shape.
To implement this, we calculate the radius (r) dynamically for each point. By varying the radius according to the formula, the distance of each point from the center changes, resulting in intricate shapes.
To make the code more readable, I split the formula into components like numerator and denominator. This approach simplifies translating mathematical equations into programming logic. Operations like absolute value, trigonometric functions (sin and cos), and exponentiation are standard in most programming languages, including JavaScript.
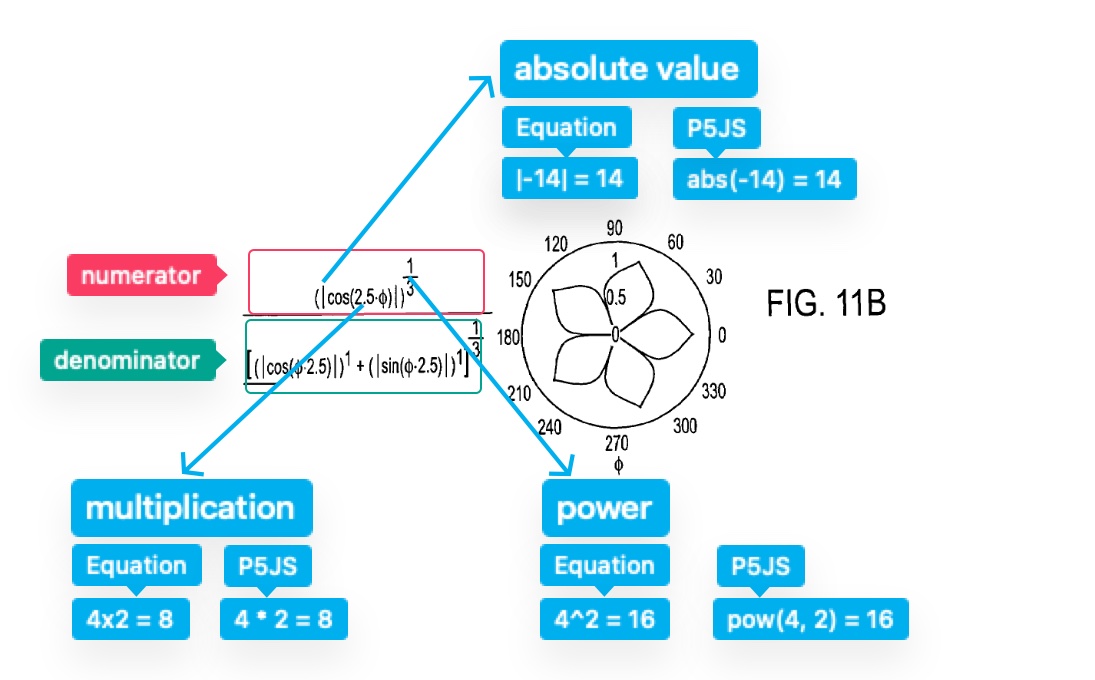
Here’s the implementation in p5.js:
const locX = width * 0.5;
const locY = height * 0.5;
const res = 100;
const perResAngle = TWO_PI / res;
const radiusScaler = 100;
for (let i = 0; i < res; i++) {
const phi = perResAngle * i; // Φ
const numerator = pow(abs(cos(2.5 * phi)), 1 / 3);
const denominator = pow(abs(cos(2.5 * phi)) + abs(sin(2.5 * phi)), 1 / 3);
const r = (numerator / denominator) * radiusScaler;
const x = locX + cos(perResAngle * i) * r;
const y = locX + sin(perResAngle * i) * r;
stroke(200, 0, 0);
strokeWeight(2);
point(x, y);
}Step 3 - Connect Points
We can achieve continues line by increasing the number of points or keep point numbers low to decrease CPU load. To achieve this, we can use beginShape(), vertex(), and endShape() methods as follows.
const locX = width * 0.5;
const locY = height * 0.5;
const res = 100;
const perResAngle = TWO_PI / res;
const radiusScaler = 100;
beginShape();
for (let i = 0; i < res; i++) {
const phi = perResAngle * i; // Φ
const numerator = pow(abs(cos(2.5 * phi)), 1 / 3);
const denominator = pow(abs(cos(2.5 * phi)) + abs(sin(2.5 * phi)), 1 / 3);
const r = (numerator / denominator) * radiusScaler;
const x = locX + cos(perResAngle * i) * r;
const y = locX + sin(perResAngle * i) * r;
vertex(x, y);
stroke(200, 0, 0);
strokeWeight(2);
point(x, y);
}
endShape(CLOSE);Step 4 - Computational Creativity
The final step is where your creativity shines! Parameterizing static values in your code opens up endless possibilities for dynamic, generative art. For example, you can encapsulate the flower-drawing logic into a drawFlower function with customizable input parameters. This allows you to layer multiple shapes with varying properties. Experiment with different parameter ranges to create unique designs with every render.
const prefix = "Genuary25_day11";
let fgCl = "#ededed"; // background color
function setup() {
createCanvas(1080, 1080); // Create the canvas 1080x1080 pixels
pixelDensity(2); // point per pixel. Increase the value to get print quality images.
}
function draw() {
background(fgCl); // Set the background color
strokeWeight(1); // set the stroke thickness
const sz = 107; // size of each flower
const rows = floor(height / (sz * 2)); // number of rows
const cols = floor(width / (sz * 2)); // number of columns on the grid
for (let i = 0; i < cols; i++) {
for (let j = 0; j < rows; j++) {
var xx = 150 + sz * 1.8 * i; // x position of each flower
var yy = 150 + sz * 1.8 * j; // y position of each flower
var initSz = random(40, sz); // initial size of the flower
var innerRad = random(0.004, 1); // initial size of the flower core
for (let k = 0; k < 5; k++) { // Regenarete flower on and on five times
drawFlower(xx, yy, initSz - k * 8, innerRad, random(0, 0.9), floor(random(1, 6)), k);
}
}
}
noLoop();
}
function drawFlower(locX, locY, sz, _innerRad, _pw, _petalNum, opDelta) {
const res = 100;
const perResAngle = TWO_PI / res;
const radiusScaler = sz;
fill(20, opDelta * 40);
stroke(20, opDelta * 20);
strokeWeight(1 + opDelta);
beginShape();
for (let i = 0; i < res; i++) {
const innerRad = _innerRad;
const phi = innerRad + perResAngle * i; // Φ
const pw = _pw;
const numerator = pow(abs(cos(_petalNum * phi)), pw);
const denominator = pow(abs(cos(_petalNum * phi)) + abs(sin(_petalNum * phi)), pw);
const r = (numerator / denominator) * radiusScaler;
const x = locX + cos(perResAngle * i) * r;
const y = locY + sin(perResAngle * i) * r;
vertex(x, y);
//point(x, y);
}
endShape(CLOSE);
}
function keyPressed() {
if (key === "s") {
saveCanvas(prefix, "png");
}
}Conclusion
Learning how to implement mathematical equations in programming is a powerful skill that unlocks endless creative potential. By delving into the process behind these equations, you’re not just relying on pre-written code or tools—you’re opening the “black box” and understanding how things work. This knowledge empowers you to adapt and extend these concepts to suit your unique artistic vision.
For artists, this technique offers the ability to create one-of-a-kind works inspired by scientific research. Resources like Google Scholar are free and filled with mathematical models that mimic real-world phenomena. By learning how to translate these models into code, you can explore new creative frontiers, blending art and science in unprecedented ways.
So why wait for someone else to write the code? Take the reins, dive into the math, and let your creativity flow.
References
Gielis, J. L. A. (2009). (54) Method And Apparatus For Synthesizing And Analyzing Patterns Utilizing Novel Super-formula Operator.
Gielis, J. L. A., & Individual. (1999, May 10). US7620527B1 - Method and apparatus for synthesizing and analyzing patterns utilizing novel “super-formula” operator - Google Patents. https://patents.google.com/patent/US7620527B1/en
GENUARY 2025 –. (n.d.). https://genuary.art/
HOW DID GENUARY? – GENUARY 2021. (n.d.). https://genuary2021.github.io/story
(P5Js Web Site, n.d.) - https://p5js.org/about/